正弦(sin)余弦(cos)正接(tan)の求め方



高校で習う三角関数ですが、数学検定をはじめとする多くの資格で前提知識として求められます。
三角関数の基本となる、sin(サイン)・cos(コサイン)・tan(タンジェント)に関して、求め方と意味を理解しておきましょう。
意味が分かれば公式の意味や求め方もスムーズに理解できるようになります。
単位円とは
最初に正弦(\(sinθ\))・余弦(\(cosθ\))・正接(\(tanθ\))の意味について確認しましょう。
分かりやすくするために単位円と呼ばれる半径\(1\)の円を用いながら解説します。
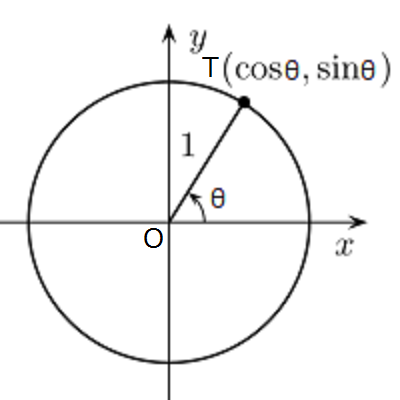
正弦\(sinθ\)
まずは正弦である\(sinθ\)の意味や求め方をおさらいしましょう。
\(sinθ\)の求め方
正弦\(sinθ\)は単位円内に作れる下記のような直角三角形OTAの高さを表しています。
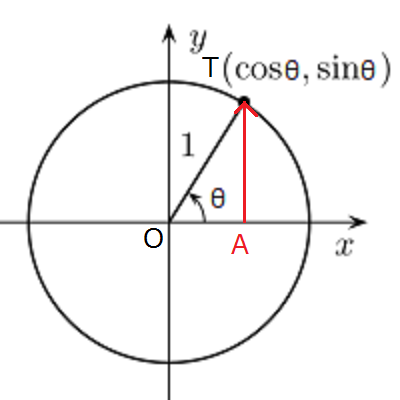
さて、ここでこの三角形OTAと相似な三角形で斜辺の長さが\(r\)倍、高さが\(y\)の三角形OT’A’を考えてみます。
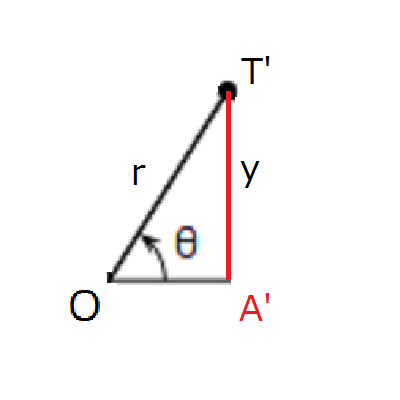
三角形OT’A’は高さが\(y\)、斜辺の長さが\(r\)対して、三角形OTAは高さが\(sinθ\)、斜辺が\(1\)なので、相似の関係であることを考慮するとそれぞれの辺の長さの関係は\(y:r=sinθ:1\)となることが分かります。
この式を解くと\(sinθ=\frac{y}{r}\)が得られます。
これで\(sinθ\)をそれ以外の値である\(y\)と\(r\)を用いて表すことができました。
主要な値だけ下にまとめておきます。
| \(θ\) | \(0\) | \(\frac{π}{6}\) | \(\frac{π}{4}\) | \(\frac{π}{3}\) | \(\frac{π}{2}\) |
| \(sinθ\) | \(\frac{\sqrt{0}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{4}}{2}\) |

正弦の角度を変えると
ここで少しθを変えてみましょう。
x軸対称
まずx軸に鏡を置いて上下が反転した場合を考えてみます。
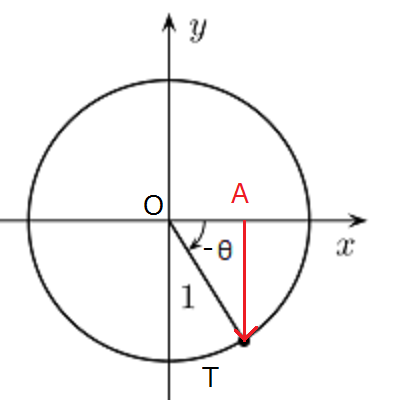
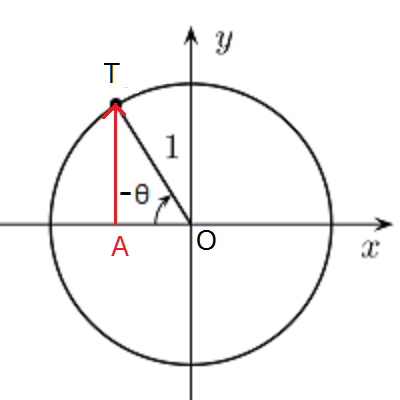
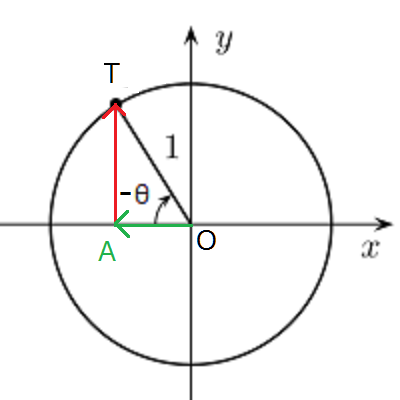
Tの位置が\(0^{\circ}\)地点から右回りにまわるので動く角度は\(-θ\)とあらわし、このときの直角三角形OTAの高さは\(sin(-θ)\)と表せます。
このときの矢印はx軸から負の方向に向かっており、矢印の大きさは\(sinθ\)と全く同じです。
したがって、\(sin(-θ)=-sinθ\)が得られます。
y軸対称
次にy軸に鏡を置いて左右反転した場合を考えてみましょう。
Tの位置が\(0^{\circ}\)地点ではなく、\(180^{\circ}\)地点から\(θ\)右回りに回るので、直角三角形OTAの高さは\(sin(180^{\circ}-θ)\)と表せます。
また、度数法である\(180^{\circ}\)は弧度法で\(\pi\)と表せるので、\(sin(180^{\circ}-θ)\)は今後\(sin(\pi-θ)\)と表記します。
このときの矢印はx軸から正の方向に向かっており、矢印の大きさは\(sinθ\)と全く同じです。
したがって、\(sin(\pi-θ)=sinθ\)が得られます。
正弦の練習問題
正弦について、練習問題で確認しておきましょう。
次の\(sinθ\)の値を求めよ。
- \(sin45^{\circ}\)
- \(sin\pi\)
- \(sin-\frac{π}{3}\)
正弦のまとめ
正弦においては以下の点を押さえておきましょう。
- \(sinθ=\frac{y}{r}\)
- \(sin(-θ)=-sinθ\)
- \(sin(\pi-θ)=sinθ\)
余弦\(cosθ\)
次に余弦\(cosθ\)の意味や求め方も確認しましょう。
\(cosθ\)の求め方
余弦である\(cosθ\)は単位円内に作れる下記のような直角三角形OTAの底辺の長さを表しています。
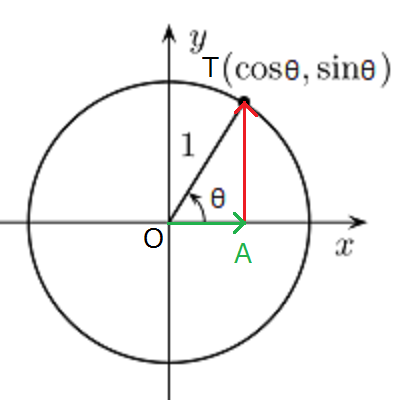
さて、ここでこの三角形OTAと相似な三角形で斜辺の長さが\(r\)倍、底辺の長さが\(x\)の三角形OT’A’を考えてみます。
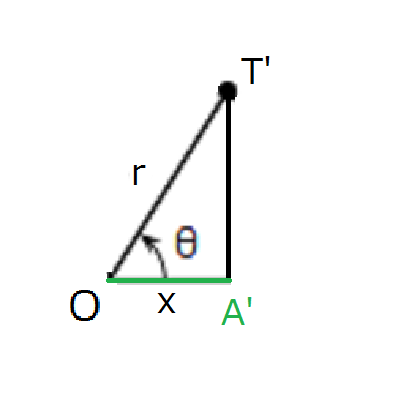
三角形OT’A’は底辺の長さが\(x\)、斜辺の長さが\(r\)対して、三角形OTAは底辺の長さが\(cosθ\)、斜辺が\(1\)です。相似の関係であることを考慮すると、それぞれの辺の長さの関係は\(x:r=cosθ:1\)となることが分かります。
この式を解くと\(cosθ=\frac{x}{r}\)が得られます。
これで\(cosθ\)をそれ以外の値である\(x\)と\(r\)で表すことができました。
主要な値だけ下にまとめておきます。
| \(θ\) | \(0\) | \(\frac{π}{6}\) | \(\frac{π}{4}\) | \(\frac{π}{3}\) | \(\frac{π}{2}\) |
| \(cosθ\) | \(\frac{\sqrt{4}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{0}}{2}\) |

余弦の角度を変えると
今度は余弦のθの値をいじってみましょう。
x軸対称
まずx軸に鏡を置いて上下が反転した場合を考えてみます。
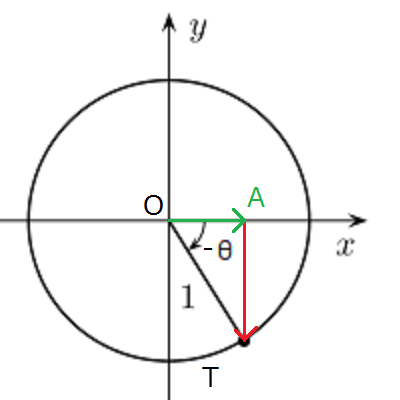
Tの位置が\(0^{\circ}\)地点から右回りにまわるので動く角度は\(-θ\)とあらわし、このときの直角三角形OTAの底辺の長さは\(cos(-θ)\)と表せます。
このときの矢印はy軸から正の方向に向かっており、矢印の大きさは\(cosθ\)と全く同じです。
したがって、\(cos(-θ)=cosθ\)が得られます。
y軸対称
次にy軸に鏡を置いて左右反転した場合を考えてみましょう。
Tの位置が\(0^{\circ}\)地点ではなく、\(\pi\)地点から\(θ\)右回りに回るので、直角三角形OTAの底辺の長さは\(cos(\pi-θ)\)と表せます。
このときの矢印はy軸から負の方向に向かっており、矢印の大きさは\(cosθ\)と全く同じです。
したがって、\(cos(\pi-θ)=-cosθ\)が得られます。
余弦の練習問題
次の\(cosθ\)の値を求めよ。
- \(cos90^{\circ}\)
- \(cos\pi\)
- \(cos-\frac{π}{2}\)
余弦のまとめ
余弦で押さえておくべきポイントは以下の通りです。
- \(cosθ=\frac{x}{r}\)
- \(cos(-θ)=cosθ\)
- \(cos(\pi-θ)=cosθ\)
正接\(tanθ\)
\(sinθ\)と\(cosθ\)を見たので最後に\(tanθ\)も見てみましょう。
\(tanθ\)の求め方
最後に、正接\(tanθ\)についても意味を解説します。
三角形OTAにおいて正弦は高さ、余弦は底辺の長さでした。
では正接はと問われれば、それはずばり三角形OTAにおける斜辺OTの傾きです。
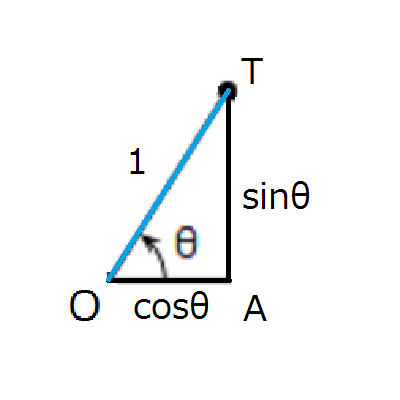
傾きであって斜辺OTの長さとは異なることに注意してください。
傾きの求め方は高さを底辺の長さで割れば良いです。三角形OTAにおいては高さは\(sinθ\)、底辺の長さは\(cosθ\)でした。
したがって、\(tanθ=\frac{sinθ}{cosθ}\)となります。
また、三角形OT’A’においては高さは\(y\)、底辺の長さは\(x\)です。
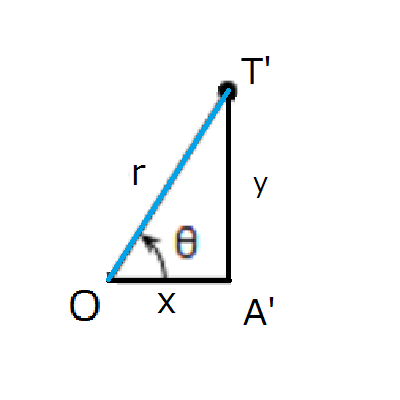
したがって\(tanθ=\frac{x}{y}\)も同時に成立します。
三角形OTAと三角形OT’A’が相似の場合、\(\frac{sinθ}{cosθ}=\frac{y}{x}\)が成立するので一度確認してみてください。
| \(θ\) | \(0\) | \(\frac{π}{6}\) | \(\frac{π}{4}\) | \(\frac{π}{3}\) | \(\frac{π}{2}\) |
| \(sinθ\) | \(\frac{\sqrt{0}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{4}}{2}\) |
| \(cosθ\) | \(\frac{\sqrt{4}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{0}}{2}\) |
| \(tanθ\) | \(0\) | \(\frac{1}{\sqrt{3}}\) | \(\frac{\sqrt{2}}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{1}\) | 定義なし(0で割れないため) |
正接の練習問題
正接についても練習問題を通して値を確認しておきましょう。
次の\(tanθ\)の値を求めよ。
- \(tan0^{\circ}\)
- \(tan\frac{π}{2}\)
- \(tan-\frac{π}{3}\)
正接のまとめ
正接におけるポイントは以下の通りです。
- \(tanθ=\frac{sinθ}{cosθ}\)
- \(tanθ=\frac{y}{x}\)
正弦・余弦・正接から分かること
\(sinθ\)・\(cosθ\)・\(tanθ\)が分かったところでもう一歩踏み込んで、これらの関係を組み合わせることで得られる値や等式を紹介しておきます。
どれも必須なので、最悪値を忘れても意味を覚えていつでも導き出せるようにしておきましょう。
\(sin^2θ+cos^2θ=1\)
\(sinθ\)の2乗と\(cosθ\)の2乗を足すと1になります。
(一般的に三角関数の2乗は\(sinθ^2\)とは書かずに\(sin^2θ\)と書きます。)
これは先ほどの単位円を見ていただければ分かるのですが、三角形OATの斜辺は単位円の半径なので、長さは\(θ\)の値に寄らず常に1になります。
そして三角形OATは高さが\(sinθ\)、底辺が\(cosθ\)の直角三角形です。
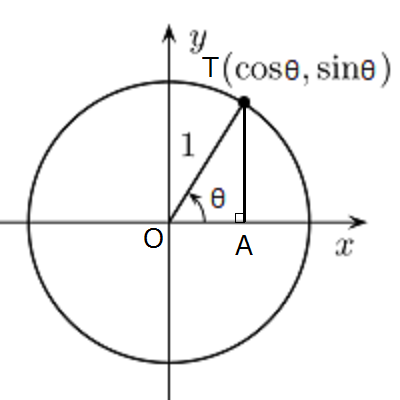
このことから三平方の定理より\(sin^2θ+cos^2θ=1^2=1\)が導けます。
\(tan^2θ+1=\frac{1}{cos^2θ}\)
なぜわざわざこんな変形をしなければいけないのかと思われがちですが、この変形は後々三角関数を微分したり積分したりするときに必要になります。
変形の流れとしては以下のように変形できます。
\(tan^2θ+1\)
\(=\frac{sin^2θ}{cos^2θ}+1\)
\(=\frac{sin^2θ}{cos^2θ}+\frac{cos^2θ}{cos^2θ}\)
\(=\frac{1}{cos^2θ}\)
正弦・余弦・正接から分かることのまとめ
正弦・余弦・正接から分かることをまとめると以下のようになります。
- \(sin^2θ+cos^2θ=1\)
- \(tan^2θ+1=\frac{1}{cos^2θ}\)
正弦・余弦・正接に関するよくある質問

- 90度の正弦・余弦・正接の値を教えてください。
- sin90°=1・cos90°=0・tan90°=解なしです。
- 180度の正弦・余弦・正接の値を教えてください。
- sin180°=0・cos180°=-1・tan180°=0です。
- 正弦・余弦・正接の意味を教えてください。
- 正弦は単位円内に作れる直角三角形の高さ、余弦は底辺の長さ、正接は傾きを意味します。
正弦・余弦・正接まとめ
\(sin\)・\(cos\)・\(tan\)の求め方を問うような初歩的な問題は試験であまり出ません。しかし、これらの根本的な意味を理解していないと混乱することもあります。
三角関数を用いる場面は多いので、これらの意味を理解した上で問題を解けるようにしておきましょう。

福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
経理4年/インフラエンジニア7年(内4年は兼務)/ライター5年(副業)
簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断修得者 など





ディスカッション
コメント一覧
まだ、コメントがありません