[FP3級]6つの係数[無料講座・例題付き!]

今回はFP3級で学習する6つの係数について学習します。



6つの係数
「現在の金額を複利で運用した場合の一定期間後の金額」だったり、「数年後に買いたいものがあるからその額に達するまでに毎年いくらずつ積み立てればよいか」などを求める際は次の係数を用いると一瞬で求めることができます。
※期間5年の場合の係数表
| 1% | 2% | 3% | 4% | 5% | |
| 終価係数 | 1.0510 | 1.1041 | 1.1593 | 1.2167 | 1.2763 |
| 現価係数 | 0.9515 | 0.9057 | 0.8626 | 0.8219 | 0.7835 |
| 年金終価係数 | 5.1010 | 5.2040 | 5.3091 | 5.4163 | 5.5256 |
| 減債基金係数 | 0.1960 | 0.1922 | 0.1884 | 0.1846 | 0.1810 |
| 資本回収係数 | 0.2060 | 0.2122 | 0.2184 | 0.2246 | 0.2310 |
| 年金現価係数 | 4.8534 | 4.7135 | 4.5797 | 4.4518 | 4.3295 |
6つの係数としては
- 終価係数
- 現価係数
- 年金終価係数
- 減債基金係数
- 資本回収係数
- 年金現価係数
があります。一つずつ確認していきましょう。
終価係数
現在の金額を複利で運用した場合に、一定期間後にいくらになるかを求める場合に用いる係数を、終価係数と呼びます。
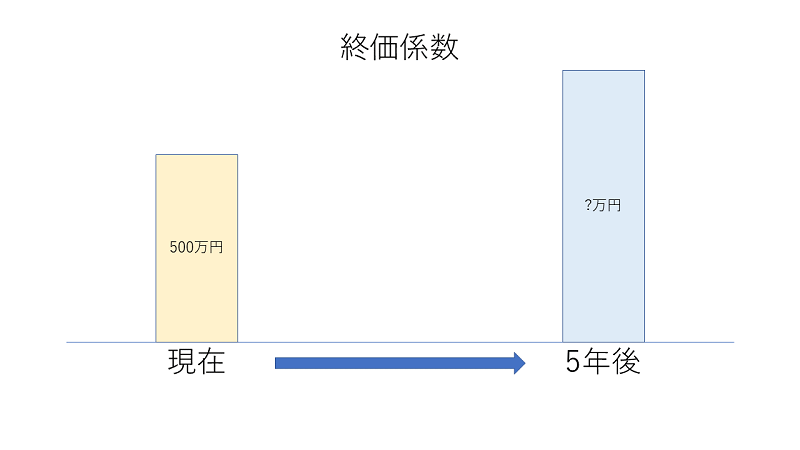
例:500万円を年利3%で運用した場合の5年後の金額はいくらか
解:5,000,000円×1.1593=5,796,500円
現価係数
一定期間後に一定金額に達するために必要な元本を求める場合に用いる係数を、現価係数と呼びます。
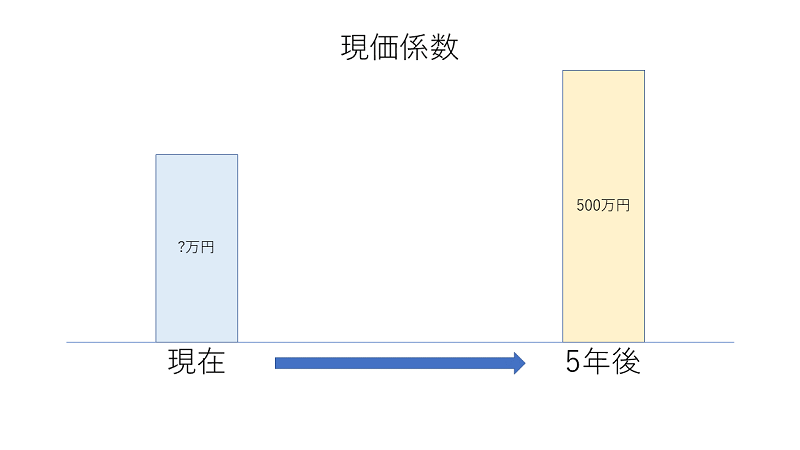
例:年利3%で5年後に500万円を用意するためには、元本がいくら必要か
解:5,000,000円×0.8626=4,313,000円
年金終価係数
毎年一定金額を積立てた場合に、一定期間後の元利の合計を求める場合に用いる係数を年金終価係数と呼びます。
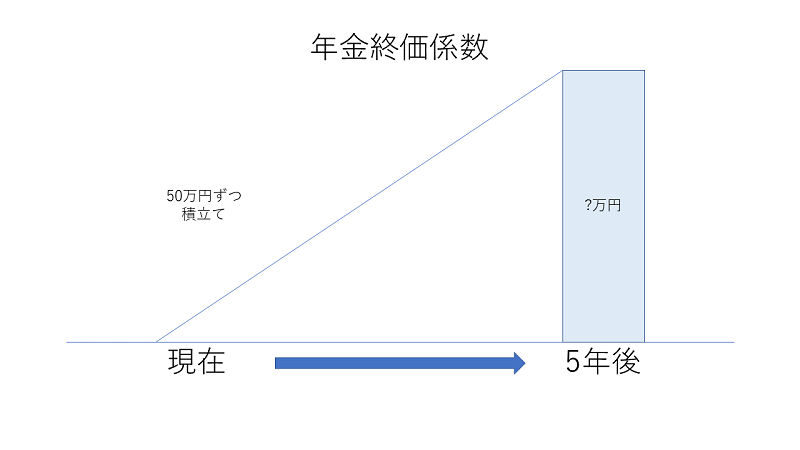
例:年利3%、毎年50万円を5年間積立てた場合の5年後の金額はいくらか
解:500,000円×5.3091=2,654,550円
減債基金係数
一定期間後に一定金額を用意するための、毎年の積立額を計算するための係数を減債基金係数と呼びます。
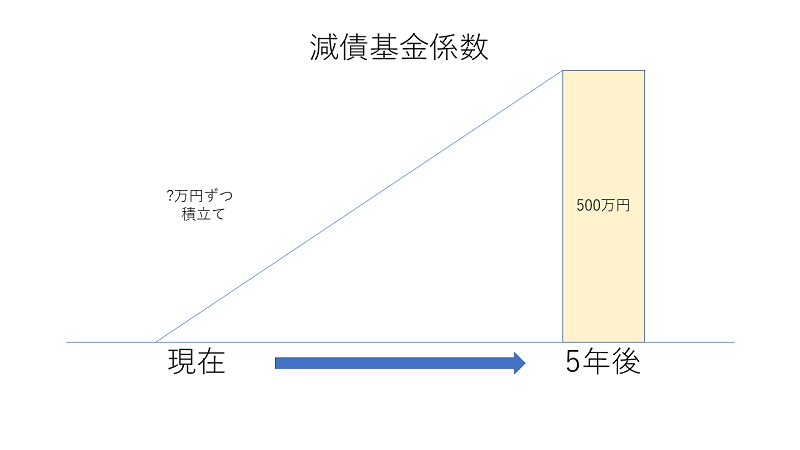
例:年利3%、5年後に500万円をよういするためには、毎年いくら積立てる必要があるか
解:5,000,000円×0.1884=942,000円
資本回収係数
現在の一定金額を一定期間で取り崩した場合の、毎年の受取額を計算するための係数を資本回収係数と呼びます。
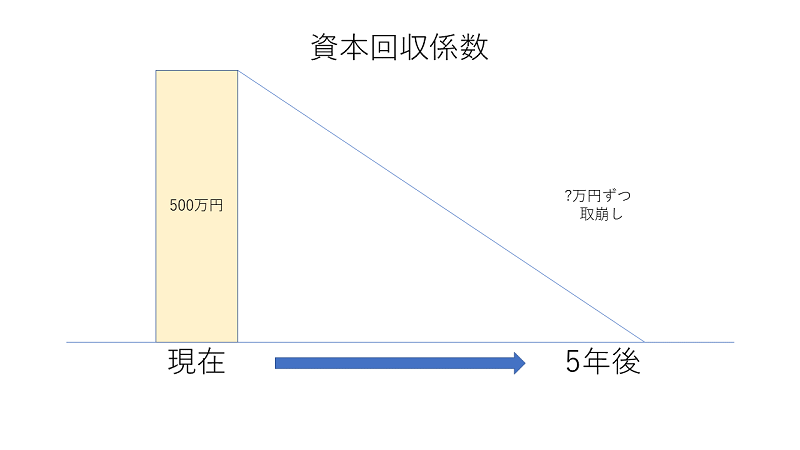
例:500万円を年利3%で運用しながら5年間で取り崩した場合の毎年の受取額はいくらか
解:5,000,000円×0.2184=1,092,000円
年金現価係数
将来の一定期間にわたって、一定額を受け取るために必要な元本を計算するための係数を年金現価係数と呼びます。
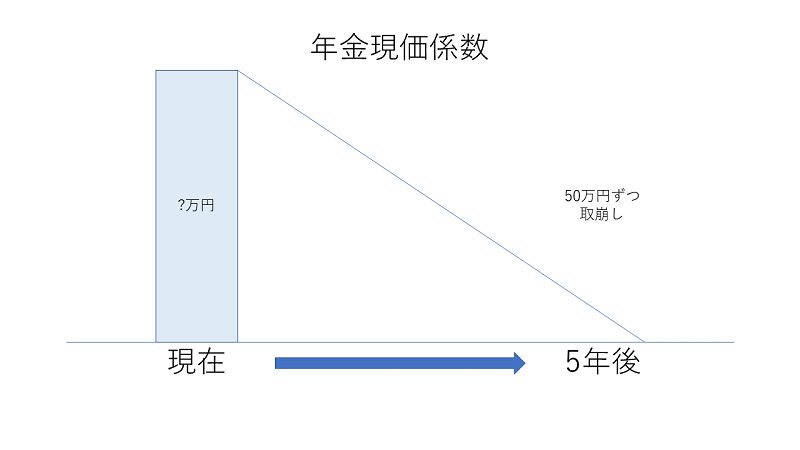
例:5年間にわたって50万円ずつ受け取る場合、年利が3%のとき、必要な元本はいくらか
解:500,000円×4.5797=2,289,850円
6つの係数・例題
実際に例題を解いて問題に慣れていきましょう。
問題
問1
元金2,000万円を、利率(年率)1%で複利運用しながら10年にわたって毎年均等に取り崩して受け取る場合、毎年の受取金額は、下記〈資料〉の係数を使用して算出すると()となる。(2018年/5月)
利率1%・期間10年間の各種係数
| 終価係数 | 減債基金係数 | 資本回収係数 |
| 1.1046 | 0.0956 | 0.1056 |
1 2,000,000円
2 2,112,000円
3 2,209,200円
問2
利率(年率)2%で複利運用しながら毎年一定額を積み立て、15年後に6,000,000円を準備する場合、毎年の積立金額は、下記〈資料〉の係数を使用して算出すると()となる。(2015年/5月)
利率2%・期間15年間の各種係数
| 原価係数 | 資本回収係数 | 減債基金係数 |
| 0.7430 | 0.0778 | 0.0578 |
1 297,200円
2 346,800円
3 466,800円
問3
元金60万円を、年利率2%で10年間にわたり毎年積み立てる場合、10年後の元利合計額を係数の1つを使用して算出するには、()を利用するとよい。(2009年/1月)
1 年金終価係数
2 終価係数
3 資本回収係数
解説(クリックで展開)
6つの係数・まとめ
今回は6つの係数について学習しました。
これらの計算問題は毎年必ず1問は出題されます。どの状況でどの係数を用いるのかをしっかりと押さえておきましょう。

次回は教育資金について学習します。

福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
経理4年/インフラエンジニア7年(内4年は兼務)/ライター5年(副業)
簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断修得者 など







ディスカッション
コメント一覧
まだ、コメントがありません